Apply Operations to an Array

Link to the problem: Apply Operations to an Array

Understanding the problem

The problem requires modifying an array in two steps. First, if two consecutive elements are equal, the left element is doubled, and the right element is set to 0. This transformation occurs sequentially as we traverse the array. After this step, all the zeros generated need to be moved to the end of the list while preserving the order of the nonzero elements.

Approach

The given problem consists of two steps that need to be completed efficiently. In the first step, we iterate through the nums array and apply an operation where, if nums[i] == nums[i+1], we multiply nums[i] by 2 and set nums[i+1] to 0. Otherwise, we skip the operation and move to the next element. This step can be achievedin O(n) time complexity by simply traversing the array once and performing the necessary modification.

After this, we need to move all the zeros generated to the end of the list. This can be done using the two-pointer method, where we keep a pointer to track the next zero, and swap it with a non-zero element when encountered. This ensures that all non-zero values are shifted forward while pushing the zeros to the right. Since this method runs in a single pass, its time complexity is O(n) as well.

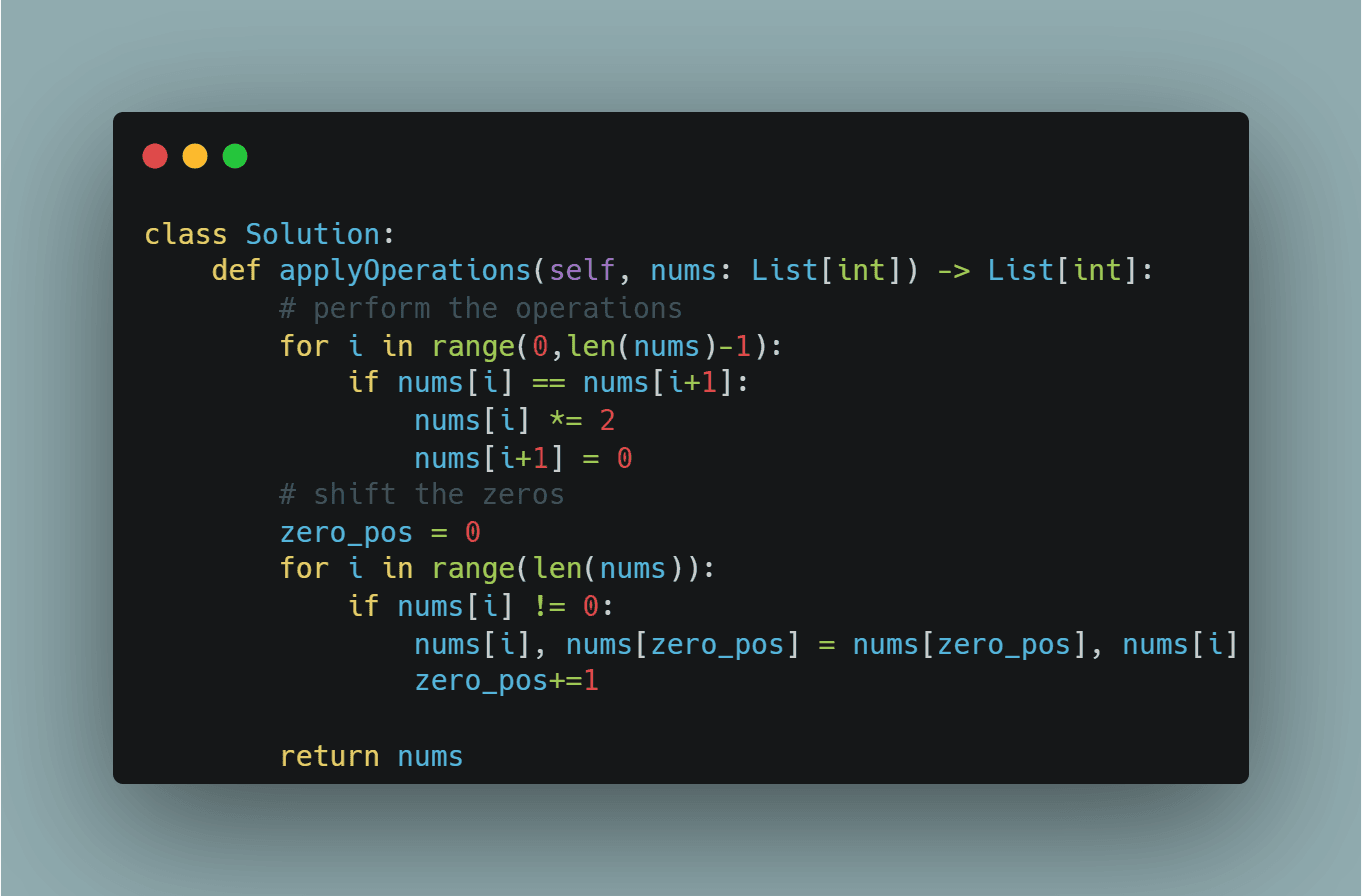
The code for the solution is as below:

class Solution:
    def applyOperations(self, nums: List[int]) -> List[int]:
        # Time Complexity: O(n)
        # Space Complexity: O(1)        
        # perform the operations
        for i in range(0,len(nums)-1):
            if nums[i] == nums[i+1]:
                nums[i] *= 2
                nums[i+1] = 0
        # shift the zeros
        zero_pos = 0
        for i in range(len(nums)):
            if nums[i] != 0:
                nums[i], nums[zero_pos] = nums[zero_pos], nums[i]
                zero_pos+=1

        return nums

Complexity Analysis

The first step, where we modify elements based on their adjacent values, runs in O(n) since we process each element once. The second step, which moves zeros to the end using the two-pointer method, also runs in O(n). Since both operations are performed sequentially, the overall time complexity remains O(n) + O(n) = O(n)

The solution operates in-place, meaning no additional data structures are used beyond a few extra variables for tracking indices. Therefore, the space complexity is O(1).